Distribución de los comandos más utilizados
Una de esas combinaciones de comandos curiosas es aquella que nos devuelve un listado de los comandos más utilizados ordenados por frecuencia, en este caso limitado a los más frecuentes:
$ history | awk '{a[$2]++} END {for (i in a) { print a[i] " " i }}' | sort -rn | head
62 cd
50 sudo
45 vim
39 ls
32 ssh
25 wget
23 memento.sh
23 cat
9 curl
9 man
A partir de estos datos, podemos obtener una distribución de su frecuencia de uso en relación al número total de comandos diferentes utilizando el paquete estadístico R:
$ history | awk '{a[$2]++}END{for(i in a){print a[i] " " i}}' | sort -rn > cmd_hist.txt
$ R --no-save << EOF
jpeg('cmd_hist.jpg')
cmd<-read.table('cmd_hist.txt')
par(cex=1.2)
plot(log(1:length(cmd[,1])),log(cmd[,1]),
pch=20,
xlab='log(Rank)',
ylab='log(frequency)')
fit<-lm(log(cmd[,1])~log(1:length(cmd[,1])))
abline(fit,lty=2)
EOF
Esta es la imagen resultante:
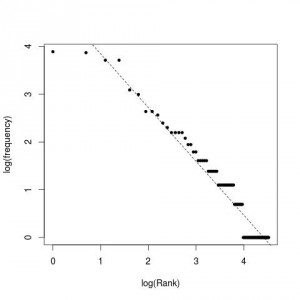
Se cumple que un reducido número de comandos se repiten la mayoría de las veces.
En particular, aunque el historial en este caso contiene 500 entradas, para los comandos más utilizados sólo se han utilizado unos 90 comandos diferentes:
$ echo $HISTSIZE
500
$ history | wc -l
500
$ history | awk '{a[$2]++}END{for(i in a){print a[i] " " i}}' | sort -rn | wc -l
87
La diferencia estriba en que hay comandos que se utilizan repetidamente pero con diferentes argumentos.
Distribución de la longitud del nombre de los comandos
De la misma manera que se calcula la distribución de la frecuencia de los comandos más utilizados, podemos calcular la distribución de la longitud de los comandos disponibles.
Si estamos en el terminal, en una línea nueva, sin haber escrito nada, y pulsamos dos veces el tabulador (ejecutamos el autocompletado), nos preguntara si queremos mostrar todas las posibilidades. Algo así:
$ [TAB][TAB]
Display all 6472 possibilities? (y or n)
Estas posibilidades son cada uno de los programas incluidos en el path del sistema, así como comandos propios del shell o alias que hayamos definido. Si nos fijamos únicamente en los programas a lo que se puede acceder desde el path:
$ for p in $(sed 's/:/\n/g' <<< $PATH); do
for cmd in $(find $p -maxdepth 1 -executable -printf '%p\n'); do
# remove prefix
cmd=${cmd##*/}
echo "${#cmd} $cmd"
done
done | sort -rn > cmd_len.txt
$ wc -l cmd_len.txt
5838 cmd_len.txt
Si queremos obtener la distribución de la longitud de sus nombres, podemos ejecutar:
$ R --no-save << EOF
jpeg('cmd_len.jpg')
cmd<-read.table('cmd_len.txt')
par(cex=1.2)
plot(log(1:length(cmd[,1])),log(cmd[,1]),
pch=20,
xlab='log(length)',
ylab='log(frequency)')
fit<-lm(log(cmd[,1])~log(1:length(cmd[,1])))
abline(fit,lty=2)
EOF
Este es el resultado:
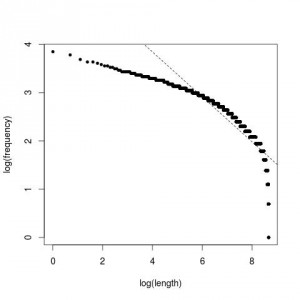
Aquí la pendiente de la curva no es tan acusada, es decir, aunque la mayoría de los comandos tienen nombres cortos y la frecuencia decrece a medida que aumenta la longitud, esta variación se produce de forma paulatina hasta el final, donde ya sí cae en picado. Esto no ocurre con los lenguajes humanos, por lo que debe haber una explicación; y quizá tenga que ver con el autocompletado. Gracias a éste, no importa tanto la longitud de un comando sino el número de pulsaciones necesarias para poder identificarlo de forma única y poder así completar su nombre con una pulsación de tabulador. También hay otros comandos que serán ejecutados mediante un click de ratón. Por esto, podría ser que se priorice claridad y legibilidad sobre longitud en los nombres de los comandos.
Distribución de palabras
Tras haber visto la distribución de la frecuencia de los comandos más utilizados y la distribución de la frecuencia de la longitud de los comandos disponibles, podemos calcular la distribución de la frecuencia de las palabras de un texto.
El texto que voy a utilizar es la Advanced Bash-Scripting Guide.
$ lynx -dump http://tldp.org/LDP/abs/html/abs-guide.html > abs-guide.txt
Separaremos las palabras del texto, convertiremos las palabras a
minúsculas, eliminaremos los signos de puntuación, las ordenaremos y las
contaremos con el siguiente script en Python, word-frequency.py:
#!/usr/bin/env python
# encoding: utf-8
import re
import sys
from string import punctuation
def main(filename):
word_freq = {}
word_list = []
try:
# After the statement is executed, the file f is always closed,
# even if a problem was encountered while processing the lines.
with open(filename) as f:
word_list = re.split('\s+', file(filename).read().lower())
except IOError as e:
print "I/O error({0}): {1}".format(e.errno, e.strerror)
except:
print "Unexpected error:", sys.exc_info()[0]
raise
for word in word_list:
word = word.translate(None, string.punctuation)
if len(word):
word_freq[word] = word_freq.get(word,0) + 1
freq_list = [(val, key) for key, val in word_freq.items()]
freq_list.sort(reverse=True)
for freq, word in reverse(freq_list):
print freq, word
def usage():
print "Usage:", sys.argv[0], " "
if __name__ == "__main__":
if len(sys.argv) < 2:
usage()
else:
main(sys.argv[1])
Creamos el archivo con el número de apariciones de cada palabra:
$ python word-frequency.py abs-guide.txt > word_freq.txt
$ wc -l word_freq.txt
26895 word_freq.txt
$ head word_freq.txt
7163 the
5448 a
4423 echo
3836 of
3805 to
2555 in
2511 is
2273 and
1794 this
1776 for
Una vez más, recurrimos a R para generar la gráfica de la distribución:
$ R --no-save << EOF
jpeg('word_freq.jpg')
cmd<-read.table('word_freq.txt')
par(cex=1.2)
plot(log(1:length(cmd[,1])),log(cmd[,1]),
pch=20,
xlab='log(Rank)',
ylab='log(frequency)')
fit<-lm(log(cmd[,1])~log(1:length(cmd[,1])))
abline(fit,lty=2)
EOF
Este es el resultado:
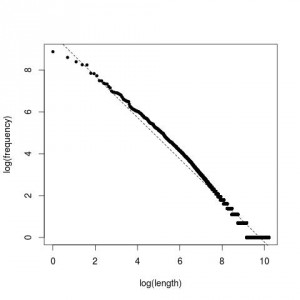
Aquí la curva es diferente al caso anterior, conforme aumenta el número de palabras distintas decrece su frecuencia de uso. Sin embargo, el texto escogido es un texto escrito en ingles, un texto técnico con ejemplos de código, por lo que tampoco podemos sacar conclusiones sobre el uso del lenguaje, o al menos no en su uso más amplio.
Para terminar, esta es la distribución que obtenemos del Quijote:
$ wget http://www.gutenberg.org/cache/epub/2000/pg2000.txt -O quijote-pg2000.txt
$ python word-length.py Descargas/quijote-pg2000.txt > quijote_freq.txt
$ wc -l quijote_freq.txt
23059 quijote_freq.txt
$ head quijote_freq.txt
20626 que
18216 de
18188 y
10363 la
9880 a
8241 en
8210 el
6345 no
4748 los
4707 se
$ R --no-save << EOF
jpeg('quijote_freq.jpg')
cmd<-read.table('quijote_freq.txt')
par(cex=1.2)
plot(log(1:length(cmd[,1])),log(cmd[,1]),
pch=20,
xlab='log(Rank)',
ylab='log(frequency)')
fit<-lm(log(cmd[,1])~log(1:length(cmd[,1])))
abline(fit,lty=2)
EOF
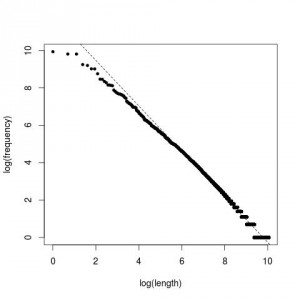
Curiosamente, se parece bastante a la anterior.
Referencias
» Distribution of Oft-Used Bash Commands » The Project Gutenberg EBook of Don Quijote » Advanced Bash-Scripting Guide